伊藤公一朗著・『データ分析の力 因果関係に迫る思考法』(光文社新書、2017年)を読んで、データ分析の入門について勉強してみました。本書は、数学が苦手な初心者でも分かりやすいように関数や数学的解説を極力避けて因果関係に迫る思考法を紹介しています。データ分析というと一般人にはあまり関係のない学問のように思えますが、知っておくだけで日常で出会う因果関係がどれほどインチキなものがおおいか愕然とするはずです。本書の一部を交えて、相関関係と因果関係について解説してみます。
「相関関係」が必ずしも「因果関係」とはいえない理由
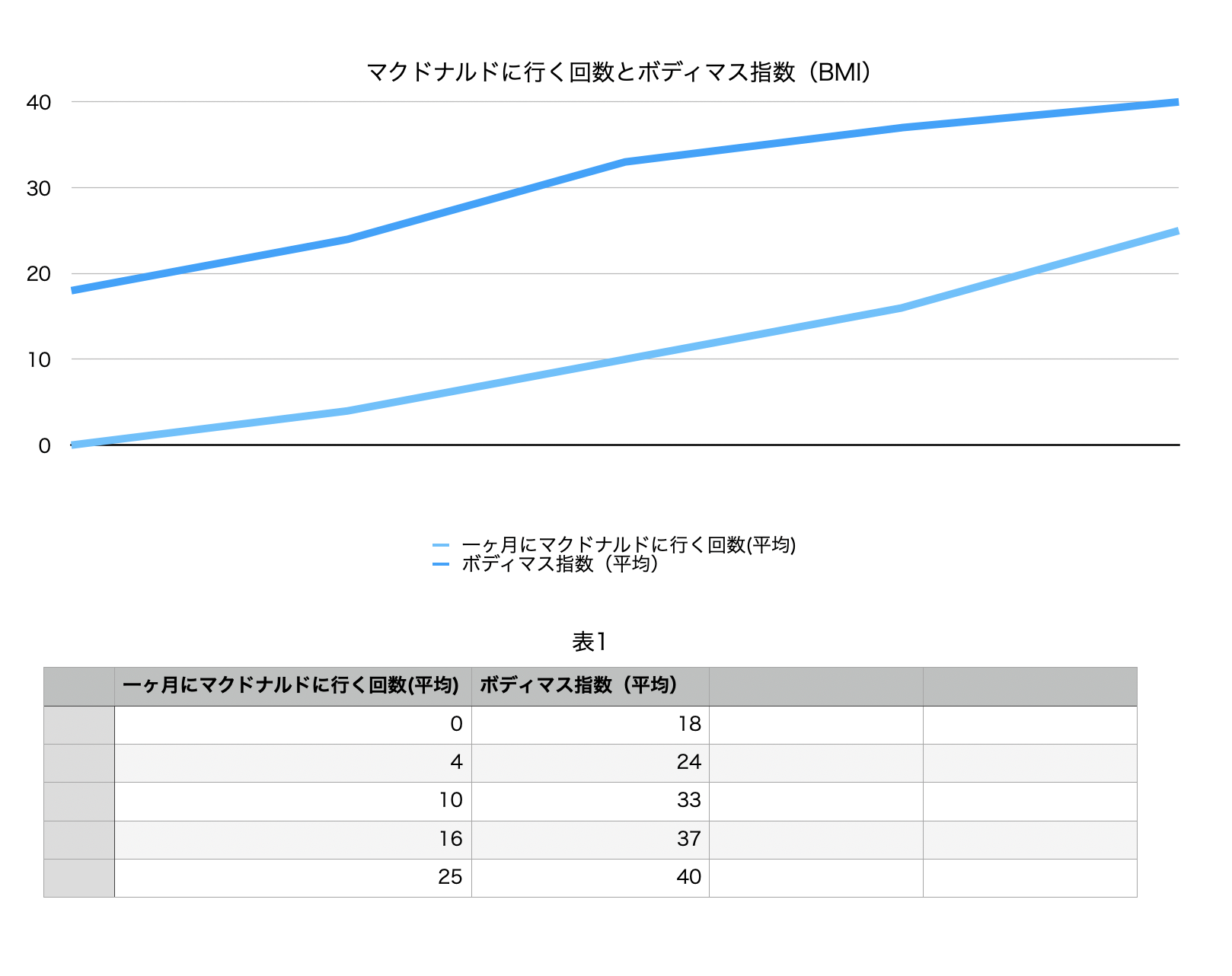
例えば、これは今簡単に思いつきで作ったグラフです。分母数や被験者については無視して、「マクドナルドに行く回数」と「BMI値(ボディマス指数)」の相関関係をグラフにしています。
実際にアメリカ人がマクドナルドに行く回数と、BMI値を数千人単位でグラフにすると同じように相関関係が見つかるかもしれません。
しかし、グラフで相関関係があるからといって因果関係があるとは言い切れず、必ずしもマクドナルドに行くことが体脂肪率に影響しているとは限らないのです。
「因果関係」は第三の要素に影響される
マクドナルドに頻繁に行く人は、ピザ屋の出前の利用回数も多いかもしれません。一日の運動量が少ないかもしれませんし、肥満ですぐに空腹を覚えるから頻繁にマクドナルドに行くのかもしれません。
マクドナルド以外の要素にBMI値が影響されたり、因果関係が逆になることもあります。たった2つの要素で因果関係を導き出すには、他の条件を完全に一致させなければなりませんが、人間でそれを証明するのは極めて難しいのです。
ネットの広告では毎日「○○を飲んだら3日で5kg痩せた?」など過激なインタビューと共に医師の姿が写っていますが、サプリメントの効果を安易に信じてはいけません。
ランダム化比較試験(RCT) と大きな分母数によって本来の因果関係が導き出せる
ランダム化比較試験(RCT)=Randomized Controlled Trialという試験方法は、創薬や研究などでは日常的に行われている技法です。比較グループと介入グループで無作為なふるい分けを行い、様々な条件が平均値の差と標準誤差が少ないことを確認して試験することによって、本来の因果関係が導き出せます。
RCTで大切なのが大きな分母数から切り分けて測定することです。先ほどの例では、マクドナルドに行く回数と肥満についての因果関係を導き出そうとしていますが、被験者が10人では正確な結果は導き出せません。アメリカ国内から様々な年齢の男女、州に住むひと、人種、学歴、職種、生活習慣の分母数を数万人〜数十万人集めると、RCTの精度が上がっていきます。
もう一つ大切なのが、RCTは強制参加型でないと正しい結果がでないということです。「ダイエットに関するアンケート調査」を街頭で参加募集すると、そもそも「ダイエットに興味のある人」に結果が偏ってしまいます。電車から降りてくる老若男女に強制的に答えさせた方が正確性がありますが、電車を利用する人という要素が追加されてしまうのが難しいところです。
電話の世論調査も偏りがある?
日本でも新聞社が「RDD(ランダム・デジット・ダイヤリング)」というコンピューターで無作為に数字を組み合わせて番号を作り、電話をかけて調査する方法で政治の世論調査を行っていますが、実はこれにも偏りがあります。
アンケート結果を見ると「固定電話100人・携帯電話100人」の調査とありますが、この時点で既に固定電話を所有している家庭に調査が偏っています。固定電話を持っている人は、携帯電話を持っている可能性も高いためです。
次に電話に出れなかった人はアンケート調査に含まれていません。仕事が多忙で電話に出れなかった人や夜勤の人などは、電話が鳴っても解答することができません。そしてもっとも重要なのが興味がない人のアンケートは完全に除外されているということです。
RDDによるアンケート結果は、固定電話もしくは携帯電話で出ることができ、さらに調査内容に関心があり協力的なデータしか収集できないということです。例えば「岸田内閣の政策について評価しますか?」という質問を電話で受けて、「解答するのも時間の無駄、面倒くさい!」と電話を切ってしまった人は結果には反映しません。
国勢調査のように、ある程度の強制力があるアンケート調査でないと偏りが出てしまいます。
「生存者バイアス」が見落とされやすい
下の絵は、分かりやすい生存バイアスの図としてよく用いられます。
帰還した飛行機の損傷部分は、命中しても安全に帰還できる箇所を示している。他の箇所に命中したものは生還できない。(画像は仮説データ)
第二次世界大戦中、統計学者エイブラハム・ウォールドは、敵の射撃による爆撃機の損失を最小限に抑える方法を検討する際に、生存者バイアスを考慮した[4]。海軍分析センターの研究者は、任務から戻った航空機が受けた損傷の研究を行い、最も損傷が多かった部位に装甲を施すよう推奨した。ウォールドはこれに対し、分析センターによる研究は任務から「生還した」航空機しか考慮していない、撃墜された爆撃機が損害評価に入っていないと述べた[4]。ウォールドは海軍に対し、帰還した航空機が損傷を受けていない部位を補強することを提案した[4]。というのは、帰還した航空機に空いた穴は、爆撃機が損傷を受けても安全に帰還できる場所を表しているからである。彼の研究は、当時のオペレーションズ・リサーチの分野では画期的なものと考えられている[5]。
https://ja.wikipedia.org/wiki/
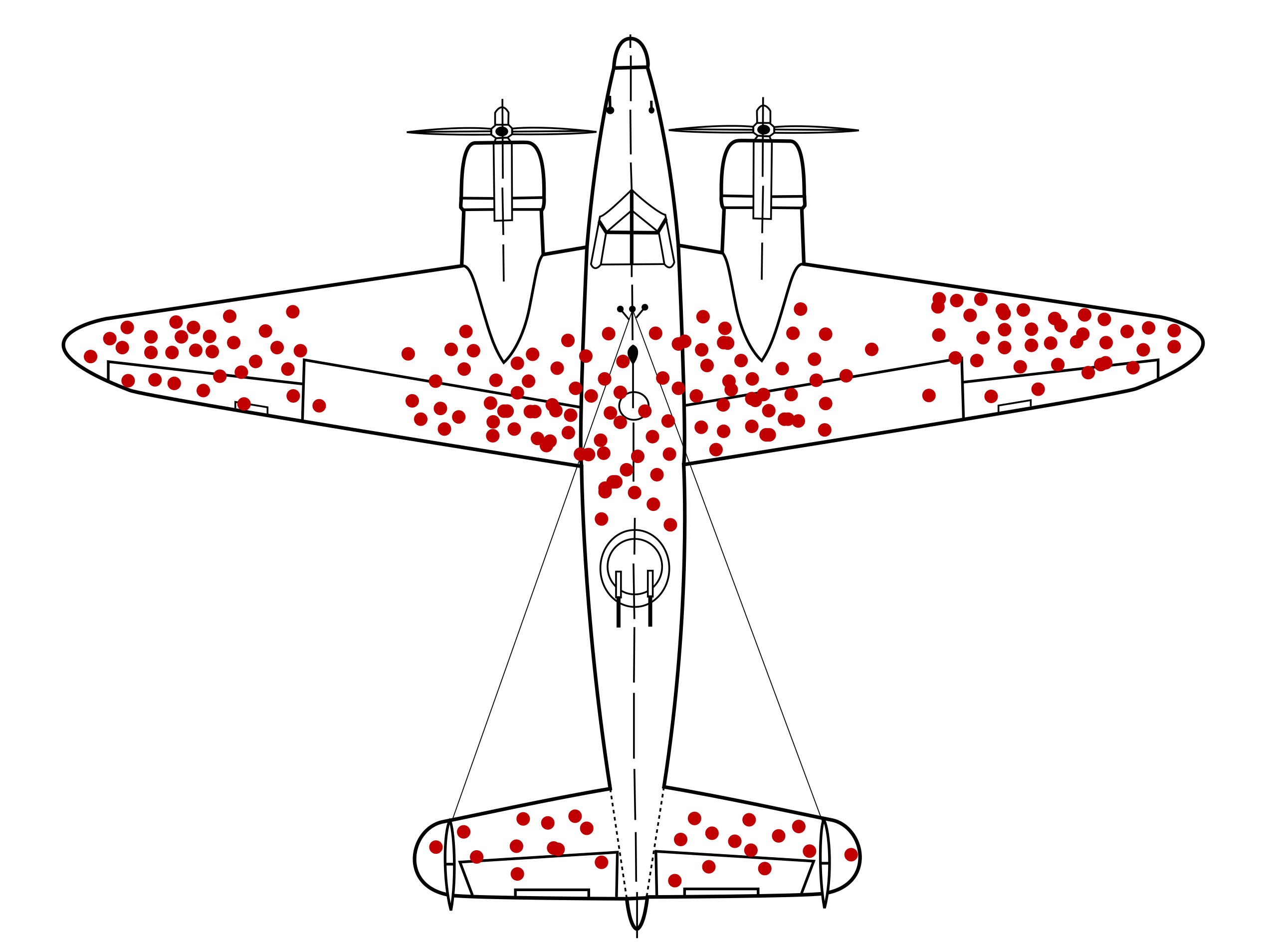
この図は基地に帰還した戦闘機が、敵に撃たれた場所を表しているものです。生存バイアスについて理解していない人だと、「翼のさきと胴体を撃たれやすいから、補強しないとならない」と頻繁に撃たれる部分を補強するように指示するかもしれません。
ところが、統計学者エイブラハム・ウォールドは「帰還した飛行機で撃たれていない場所は致命的な部分である」と判断して、玉が当たっていない部分を補強させました。これは生存バイアスがかかっていることを理解していたため正しい判断ができました。
例えば、試験に合格できた人にインタビューしても勉強方法のコツは分かるかもしれせんが、「何をすれば落ちる」かは理解できません。100人の合格者にインタビューするよりも、100人の不合格者にインタビューした方が、「何をすれば試験に落ちる」かが見えてきます。
他にも認知バイアスや正常性バイアスなどありますが、話がそれてしまうので割愛します。
先入観による因果関係の導き
本書ではオバマ大統領が選挙で使ったRCT分析の手法から、RCTが使えないときにグラフの境界線を使って擬似的に分析する「RDデザイン」、グラフの段階や頻度から結果を導き出す「集積分析」など様々な技法を初心者向けに解説しています。
「相関関係」と「因果関係」は先入観を利用した営業テクニックとして悪用されることが多いです。「コレを利用すれば、こんなに良い結果が!」と商品やサービスを売り込むのに用いられています。
悪質な営業には「それって相関関係はありますが、因果関係はありませんよね。」と西村ひろゆき氏のようにサクッと指摘できるように勉強すれば、日常生活や仕事に役立つかもしれません。



コメント